Apple - math puzzle
| Eric has a perfect spherical shaped apple. With a cilindrically shaped drill bit he removes the core of the apple. A cilindrically shaped hole remains, the center of this hole is exactly at the center of the apple. Eric measures the length of the hole with a piece of rope. It turns out to be exactly 8 cm. What is the volume of the remaining apple? |

|
Explanation
|
The funny thing of this problem is that it is not necessary to know the radius of the apple in order to solve the problem.
Let us call the radius of the apple r and that of the drill bit a. The length of the hole is 2*d. See the picture on the right-hand side, which is a cross-section of a part of the apple. The volume of the remaining apple can be obtained by calculating the volume of the part of the apple displayed in the figure, rotated along the y-axis. That volume is equal to 4 * pi * Integral[between x=a en x = r of x * (r^2 - x^2)^(1/2) dx] = 4 * pi (r^2 - a^2)^(3/2) / 3. Using the theorem of Pythagoras we have a^2 + d^2 = r^2. If we apply this result to the formula above we find V = 4 * pi * d^3 / 3. If the hole has a length of 8 cm, then d is equal to 4 cm and the volume of the remaining apple 268 cm^3. |
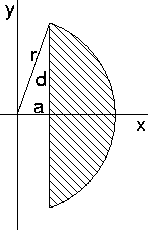
|
|
|