Platonic solids - math puzzle
| Show that there exist only five platonic solids (that are objects which are build out of the one sort of regular polygons, like the tetrahedron and the cube). Hint: use that for each solid in three dimensions it holds that the number of vertices + the number of faces is equal to the number of edges + 2. |
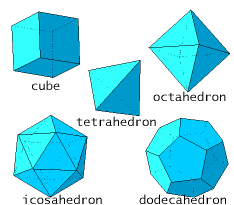
|
Explanation
Let us call the number of faces of the platonic solid F, the number of edges E and and the number of vertices V. It holds that F + V = E + 2.
A platonic solid is build out of equilateral polygons. The number of polygons is hence equal to V. Let us call the number of edges of a polygon n.
In every vertex of a platonic solid arrive an equal number of edges, let us call this number m. A tetrahedron for example is build out of 4 equilateral triangles and in each vertex 3 edges arrive, so F = 4, m = 3 and n = 3.
It now holds that the number of edges is equal to the number of faces times the number of edges of the polygon divided by two (every edge of the platonic solid is an edge of two polygons). Hence
E = F * n / 2.
The number of vertices is equal to the number of edges divided by m / 2. So
V = 2 * E / m.
Using that F + V = E + 2, we find
2 * E / m + 2 * E / n = E + 2
which can be written as
1/E = 1/m + 1/n - 1/2.
First we consider all possible platonic solids build out of equilateral triangles, so n = 3. Using the formula above we find
1/E = 1/m - 1/6
This equation has the following solutions:
m = 3, E = 3. From this it follows that V = 3 and F = 3. This is a tetrahedron.
m = 4, E = 12. From this it follows that V = 6 and F = 8. This is a octahedron.
m = 5, E = 30. From this it follows that V = 20 en F = 20. This is a icosahedron.
For m larger than 5 the equation does not have solutions because the right-hand side then becomes zero or smaller than zero, whereas the left-hand side stays always positive. Hence there are three platonic solids build out of triangles.
Now we will investigate the platonic solids build out of squares. Then n = 4 and we have to solve
1/E = 1/m - 1/4.
This equation has the following solution m = 3, E = 12. From this it follows that V = 8 and F = 6. This is a cube. For m larger than 4 this equation does not have solution. So there is only one platonic solid build out of squares.
Now the case with n = 5. Then it holds that 1/E = 1/m - 3/10
The single solution of this equation is
m = 3, E = 30. From this it follows that V = 20 en F = 12. This dodecahedron.
For n larger than 5 the formula 1/E = 1/m + 1/n - 1/2 does not have solutions. This is because 1/m + 1/n - 1/2 is then always smaller than zero, whereas 1/E stays positive. So there are no platonic solids with n > 5.
Now we have classified all platonic solids. We have shown that there are only five of them, the tetrahedron, the cube, the octahedron, the dodecahedron and the icosahedron.
A platonic solid is build out of equilateral polygons. The number of polygons is hence equal to V. Let us call the number of edges of a polygon n.
In every vertex of a platonic solid arrive an equal number of edges, let us call this number m. A tetrahedron for example is build out of 4 equilateral triangles and in each vertex 3 edges arrive, so F = 4, m = 3 and n = 3.
It now holds that the number of edges is equal to the number of faces times the number of edges of the polygon divided by two (every edge of the platonic solid is an edge of two polygons). Hence
E = F * n / 2.
The number of vertices is equal to the number of edges divided by m / 2. So
V = 2 * E / m.
Using that F + V = E + 2, we find
2 * E / m + 2 * E / n = E + 2
which can be written as
1/E = 1/m + 1/n - 1/2.
First we consider all possible platonic solids build out of equilateral triangles, so n = 3. Using the formula above we find
1/E = 1/m - 1/6
This equation has the following solutions:
m = 3, E = 3. From this it follows that V = 3 and F = 3. This is a tetrahedron.
m = 4, E = 12. From this it follows that V = 6 and F = 8. This is a octahedron.
m = 5, E = 30. From this it follows that V = 20 en F = 20. This is a icosahedron.
For m larger than 5 the equation does not have solutions because the right-hand side then becomes zero or smaller than zero, whereas the left-hand side stays always positive. Hence there are three platonic solids build out of triangles.
Now we will investigate the platonic solids build out of squares. Then n = 4 and we have to solve
1/E = 1/m - 1/4.
This equation has the following solution m = 3, E = 12. From this it follows that V = 8 and F = 6. This is a cube. For m larger than 4 this equation does not have solution. So there is only one platonic solid build out of squares.
Now the case with n = 5. Then it holds that 1/E = 1/m - 3/10
The single solution of this equation is
m = 3, E = 30. From this it follows that V = 20 en F = 12. This dodecahedron.
For n larger than 5 the formula 1/E = 1/m + 1/n - 1/2 does not have solutions. This is because 1/m + 1/n - 1/2 is then always smaller than zero, whereas 1/E stays positive. So there are no platonic solids with n > 5.
Now we have classified all platonic solids. We have shown that there are only five of them, the tetrahedron, the cube, the octahedron, the dodecahedron and the icosahedron.
|
|