What will be the probability that the price of a randomly choosen share that can be bought on the euronext stock exchange in Amsterdam, starts with the digit 1?

On a first sight, the correct answer may sound strange. The probability that the price of a randomly choosen share starts with a digit 1 is approximately about 30% and not as you might have guessed 1/9 = 11%.

With share prices, you can assume that high prices (say 1000 euro's per share) occur less often than low prices (like 10 euro's per share). But of course it is likely that there are about as many share that have a price between 9 and 10 euros, that there are between 10 and 11 euro's. So assuming the number of shares with a price of 19 euro is just a little bit less than the shares with a price of 10 euro, you can say that the the probability that the price lies between 10 and 19 euro is a little bit less than 10 times the probability that the price lies between 9 and 10 euro's. The same argument is valid for higher prices, the probability that the prize lies between 100 and 199 euro's is about 10 time the probability that the prize lies between 90 and 99 euro's. Since higher prizes occur less often, this implies that the probability that a prize starts with digit 1 is about then times as big as the probability that the prize starts with digit 9. Prizes which start with digit 1 will hence occur more often.

Now a somewhat more mathematical approach. Call the probability density function for share prizes P(x), where x is an amount in euro's. This implies that the probability that the stock prize lies between x1 and x2 is equal to

Of course it holds that

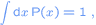
in other words, the total probability equals 1. If one would convert the share prizes into dollars (y) then the probability density function in dollars will be P(y) = P(k * x), where 1 dollar is equal to k euro's. It holds that

in other words, the probability that a share prize lies between 1 and 2 dollars is some constant time the probability that the share prize lies between 1 and 2 euro's. The probability density is

So

By differentiating the equation P(k * x) = 1 / k P(x) to x and putting k to 1, one can find that x P'(x) = - P(x). From this equation it follows that P(x) = c / x. Here c is a constant which can be found by normalizing the probability density function to 1.

Using this probability function it is possible to calculate the probability that a share prize starts with digit B. That will then be

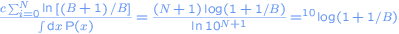
For B = 1 we find log 2 = 0.3 = 30%. The probability that a share prize starts with digit 1 is about 30%. This phenomenom is called the law of Benford and is valid for much more things than only share prizes. For example with the number of inhabitants of a randomly choosen country, or the number of leaves from a randomly choosen tree in the forest.

Below, you'll find a table with the probabilities on first digits 1 to 9 of the share prizes of Friday February 18, 2005.

digit   probability       prediction     
1         0.263682         0.301030
2         0.243781         0.176091
3         0.139303         0.124939
4         0.089552         0.096910
5         0.129353         0.079181
6         0.049751         0.066947
7         0.014925         0.057992
8         0.059701         0.051153
9         0.009950         0.045757

From the table, one can clearly see that the probability on digit 1 is much larger than on the other digits and that it is about 30%.

Of course with this knowledge you probably can't make any money with trading shares. However, you might use it for a good bet with somebody.