Rat race - math puzzle
|
On the yearly fair you can play as often as you like the game "rat race". In this game a rat is freed at the beginning of a circuit. The rat will then run to hole A, B or C, every hole with equal chance. Before the rat is freed, you can bet any amount you like on the hole the rat will run into. If you choose the right hole, you'll get back twice the amount you've put a stake. If you're wrong you loose your money. Suppose you carry an infinite amount of money. Will you in that case always loose money playing this game, or does there exist a strategy to win money. Does this strategy also work in the more realistic situation when you carry a limited amount of money or if there is a maximum limit on the bet? |

|
Explanation
First, consider the case that you can bet what you like and that you supposedly have an unlimited amount of money.
The probability that the rat goes through hole A, B or C is of course 1/3. But this is not so important, if you're always betting on hole A, at some point you will win.
Now the way to play. First gamble with 1 dollar on hole A. If you're right you win 1 dollar and stop playing. If you're wrong you loose 1 dollar. Then you should double you're stakes in the next round, so put in 2 dollars. If you're right in the second round, you'll get back 4 dollars, so you have gained 4 - 2 - 1 = 1 dollar in total. If you're wrong than you double your bet in the next round again etc.
You should double until the rat goes through hole A and then stop playing. Then eventually you will win 1 dollar. By doubling the stakes, when you win, you get all the money back you lost.
But if you dare, you can make it even more interesting. Then you should triple or enlarge your bet each time even more. For example if you start with one dollar, you multiply your bet each round with N, and the rat goes through hole A for the first time after n rounds, you will gain
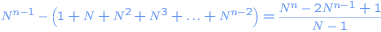
dollars. Suppose you start with one dollar, you multiply each round by 4 and after 6 rounds the rat goes through hole A. Then you'll win 683 dollars!. Easy money, right?
But unfortunately this is only theory. In reality there is a catch (thanks to Jim Loy for pointing this out), when you go to the fair, you carry only a limited amount of money. So at some point you can't multiply your bet anymore. This also happens when there is an upper amount on the money you can bet.
Now let's do a detailed anlysis. Suppose there is no such upper bound, but you carry only x dollars. The probability p that you gamble right in each round is 1/3 in this case. You multiply your bet each round with N and the first bet is 1 dollars. If you win you get back M times your bet, M = 2 in this case.
Since you carry only x dollar you can play a limited number of games. If you stay N-folding starting from 1 dollar and play n rounds until you win, you'll need
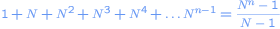
dollars in total. So the number of rounds you can play at maximum is the largest value of n for which it holds that
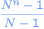
is smaller than x.
Now you can make the following table
The probability that you don't win in the n-round and have to stop is (1-p)^n. In that case you loose (N^n - 1) / (N-1) dollars.
Now we can calculate the expected amount of money S you will gain or loose. That is just the probability you win in the first round times the gain in the first round + the probability you win in the second round times the gain + .... + the probability you win in the n-th round times the gain - the probability that you loose in the n-th round times the total loss.
So we find
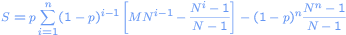
which can be simplified to
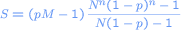
Now if p * M is smaller than 1 you will loose money. This of course is true in any realistic game. You never will get back say 3 times your bet if the chance of having it correct is only 1/2. In the rat race game p * M = 2/3 = 0.66666. So therefore, if you have enough money for playing n rounds in the rat race, you will always loose money in the end.
The probability that the rat goes through hole A, B or C is of course 1/3. But this is not so important, if you're always betting on hole A, at some point you will win.
Now the way to play. First gamble with 1 dollar on hole A. If you're right you win 1 dollar and stop playing. If you're wrong you loose 1 dollar. Then you should double you're stakes in the next round, so put in 2 dollars. If you're right in the second round, you'll get back 4 dollars, so you have gained 4 - 2 - 1 = 1 dollar in total. If you're wrong than you double your bet in the next round again etc.
You should double until the rat goes through hole A and then stop playing. Then eventually you will win 1 dollar. By doubling the stakes, when you win, you get all the money back you lost.
But if you dare, you can make it even more interesting. Then you should triple or enlarge your bet each time even more. For example if you start with one dollar, you multiply your bet each round with N, and the rat goes through hole A for the first time after n rounds, you will gain
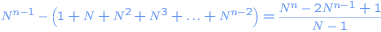
dollars. Suppose you start with one dollar, you multiply each round by 4 and after 6 rounds the rat goes through hole A. Then you'll win 683 dollars!. Easy money, right?
But unfortunately this is only theory. In reality there is a catch (thanks to Jim Loy for pointing this out), when you go to the fair, you carry only a limited amount of money. So at some point you can't multiply your bet anymore. This also happens when there is an upper amount on the money you can bet.
Now let's do a detailed anlysis. Suppose there is no such upper bound, but you carry only x dollars. The probability p that you gamble right in each round is 1/3 in this case. You multiply your bet each round with N and the first bet is 1 dollars. If you win you get back M times your bet, M = 2 in this case.
Since you carry only x dollar you can play a limited number of games. If you stay N-folding starting from 1 dollar and play n rounds until you win, you'll need
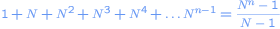
dollars in total. So the number of rounds you can play at maximum is the largest value of n for which it holds that
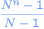
is smaller than x.
Now you can make the following table
| Round | Dollars you bet | Probability gamling right | Gain if gambled right | 1 | 1 | p | M - 1 |
| 2 | N | p(1-p) | M*N - N - 1 |
| 3 | N*N | p(1-p)^2 | M*N^2 - N^2 - N - 1 |
| .. | .. | .. | .. |
| n | N^(n-1) | p(1-p)^(n-1) | M * N^(n-1) - (N^n - 1) / (N - 1) |
Now we can calculate the expected amount of money S you will gain or loose. That is just the probability you win in the first round times the gain in the first round + the probability you win in the second round times the gain + .... + the probability you win in the n-th round times the gain - the probability that you loose in the n-th round times the total loss.
So we find
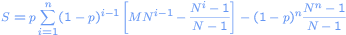
which can be simplified to
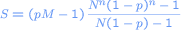
Now if p * M is smaller than 1 you will loose money. This of course is true in any realistic game. You never will get back say 3 times your bet if the chance of having it correct is only 1/2. In the rat race game p * M = 2/3 = 0.66666. So therefore, if you have enough money for playing n rounds in the rat race, you will always loose money in the end.
|
|