The walled garden - math puzzle
| A garden is surrounded by four walls, which form a rectangular trapezoid. The parallel walls have lengths of 34 and 59. An old oak grows in the middle of the garden. The owner of the garden has figured out that the distance from the four walls to the oak are exactly the same. What is the area of the garden? |
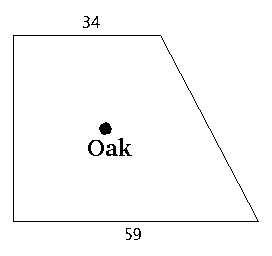
|
Explanation
|
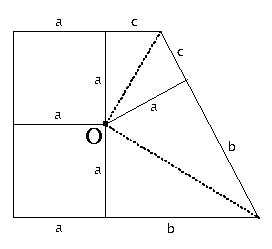
The point O (Oak) is the middle of a circle (with radius a) which just touches all walls. The area of the garden is equal to
a(2a + b + c) = 2a2 + ab + ac.
The dotted lines from O are perpendicular to each other, as a result a2 = bc. Hence, the area becomes a2 + ab + ac + bc = (a + b)(a + c). Which is 59 * 34 = 2006. |
|
|
|