- Most difficult on top
Somewhere on a sphere - math puzzle
What is the mean distance between two randomly choosen points within a sphere of radius 1?
Platonic solids - math puzzle
| Show that there exist only five platonic solids (that are objects which are build out of the one sort of regular polygons, like the tetrahedron and the cube). Hint: use that for each solid in three dimensions it holds that the number of vertices + the number of faces is equal to the number of edges + 2. |
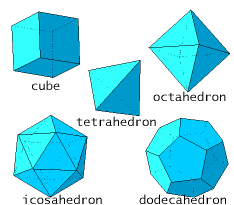
|
Divisible from 1 to 9 - math puzzle
Find a number consisting of 9 digits in which each of the digits from 1 to 9 appears only once. This number should satisfy the following requirements:
a. The number should be divisible by 9.
b. If the most right digit is removed, the remaining number should be divisible by 8.
c. If then again the most right digit is removed, the remaining number should be divisible by 7.
d. etc. until the last remaining number of one digit which should be divisible by 1.
a. The number should be divisible by 9.
b. If the most right digit is removed, the remaining number should be divisible by 8.
c. If then again the most right digit is removed, the remaining number should be divisible by 7.
d. etc. until the last remaining number of one digit which should be divisible by 1.
- Most difficult on top