- Most difficult on top
Rat race - math puzzle
|
On the yearly fair you can play as often as you like the game "rat race". In this game a rat is freed at the beginning of a circuit. The rat will then run to hole A, B or C, every hole with equal chance. Before the rat is freed, you can bet any amount you like on the hole the rat will run into. If you choose the right hole, you'll get back twice the amount you've put a stake. If you're wrong you loose your money. Suppose you carry an infinite amount of money. Will you in that case always loose money playing this game, or does there exist a strategy to win money. Does this strategy also work in the more realistic situation when you carry a limited amount of money or if there is a maximum limit on the bet? |

|
Golden rings - logic puzzle
A jeweller has three boxes: A, B and C. Each box contains three rings, which are either all made of pure gold, or all fake. The fake rings weight 1 gram less then the real ones. It is known that a least one of the boxes contains fake rings. The jeweller has a balance with three weights of exactly 1 gram. Is it possible that the jeweller finds out which box(es) contain the fake rings with weighing only once? And if so, how does she do it? (We define weighing only once that only once a situation is reached in which the balance is in equilibrium.)
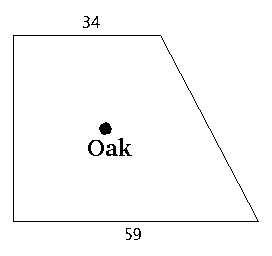
The walled garden - math puzzle
| A garden is surrounded by four walls, which form a rectangular trapezoid. The parallel walls have lengths of 34 and 59. An old oak grows in the middle of the garden. The owner of the garden has figured out that the distance from the four walls to the oak are exactly the same. What is the area of the garden? |
|
- Most difficult on top