- Easiest on top
Lockers - math puzzle
A high school has a strange principal. On the first day, he has his students perform an odd opening day ceremony:
There are one thousand lockers and one thousand students in the school. The principal asks the first student to go to every locker and open it. Then he has the second student go to every second locker and close it. The third goes to every third locker and, if it is closed, he opens it, and if it is open, he closes it. The fourth student does this to every fourth locker, and so on. After the process is completed with the thousandth student, how many lockers are open?
There are one thousand lockers and one thousand students in the school. The principal asks the first student to go to every locker and open it. Then he has the second student go to every second locker and close it. The third goes to every third locker and, if it is closed, he opens it, and if it is open, he closes it. The fourth student does this to every fourth locker, and so on. After the process is completed with the thousandth student, how many lockers are open?
Somewhere on a sphere - math puzzle
What is the mean distance between two randomly choosen points within a sphere of radius 1?
Platonic solids - math puzzle
| Show that there exist only five platonic solids (that are objects which are build out of the one sort of regular polygons, like the tetrahedron and the cube). Hint: use that for each solid in three dimensions it holds that the number of vertices + the number of faces is equal to the number of edges + 2. |
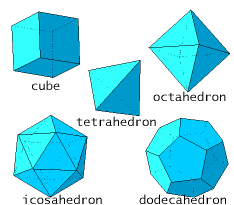
|
- Easiest on top