- Most popular on top
Rat race - math puzzle
|
On the yearly fair you can play as often as you like the game "rat race". In this game a rat is freed at the beginning of a circuit. The rat will then run to hole A, B or C, every hole with equal chance. Before the rat is freed, you can bet any amount you like on the hole the rat will run into. If you choose the right hole, you'll get back twice the amount you've put a stake. If you're wrong you loose your money. Suppose you carry an infinite amount of money. Will you in that case always loose money playing this game, or does there exist a strategy to win money. Does this strategy also work in the more realistic situation when you carry a limited amount of money or if there is a maximum limit on the bet? |

|
Keep the money rolling - math puzzle
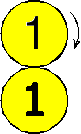
| You put two 1 dollar coins on a table, such that they touch each other (see the figure). While you fix the lower coin with your finger, you will turn the upper around it (without slipping). Somewhat later the moving coin will be back in his original position. How many rotations on his midpoint did the moving coin make? |
|
Painting stairs - math puzzle
|
To enter the house of the professor, you first have to walk up a stairs which consists out of twenty steps. The professor thinks his stairs are boring so he decides to paint them. He buys two colors, yellow and green. Every step will be either painted yellow or green and moreover the professor does not want to have two yellow steps directly after each other. In how many ways can the professor paint his stairs? And what is the name of the professor? |
|
- Most popular on top